Een satelliet lanceren

14 april • Ad Mooldijk

Een raket die omhoog gaat blijft een mooi gezicht. Je vraagt je echter wel eens af waarom die raketten zo ontzettend groot moeten zijn om een redelijk kleine satelliet in een baan om de aarde te krijgen. Het grote probleem wat om de hoek komt kijken, is, dat de brandstof die nodig is op 1000 km hoogte, wel eerst op die hoogte gebracht moet worden, waar ook brandstof voor nodig is. De ingenieurs, die de raketten ontwerpen voor het omhoog brengen van satellieten moeten daar rekening mee houden. Berekeningen voor de benodigde brandstof zullen niet gemakkelijk zijn, omdat de brandstof zelf ook weer brandstof nodig heeft om omhoog te komen. De natuurkundige principes zelf zijn echter niet zo moeilijk.

Dit soort problemen zijn daarom ideaal om in een model ondergebracht te worden.In dit deel ga je met behulp van modelomgeving onderzoeken wat de invloed is van de hoeveelheid brandstof op de te bereiken hoogte van de raket.

Een inleidende proef.

Een speelgoedraket kun je zelf maken van een petfles en stuwkracht geven op de volgende manier:

Vul de raket voor een deel met water.
Pomp lucht in de raket, waardoor het water onder druk komt te staan.
Laat de raket los schieten de lucht in
Onderzoek , als de raket werkt, hoe de hoeveelheid water (met evenveel lucht, dus evenveel pompslagen) de hoogte van de raket beïnvloedt.

Een eerste model voor een raket.

Om een model voor een raket te maken, moet je eerst een paar zaken op een rijtje zetten. Het beste kun je het probleem stapje voor stapje aanpakken.

Het model RAKET01 laat een raket met snelheid omhoog gaan, zonder stuwkracht. Het is zo gemaakt, dat je vanaf het bewegingsdeel niets hoeft te veranderen.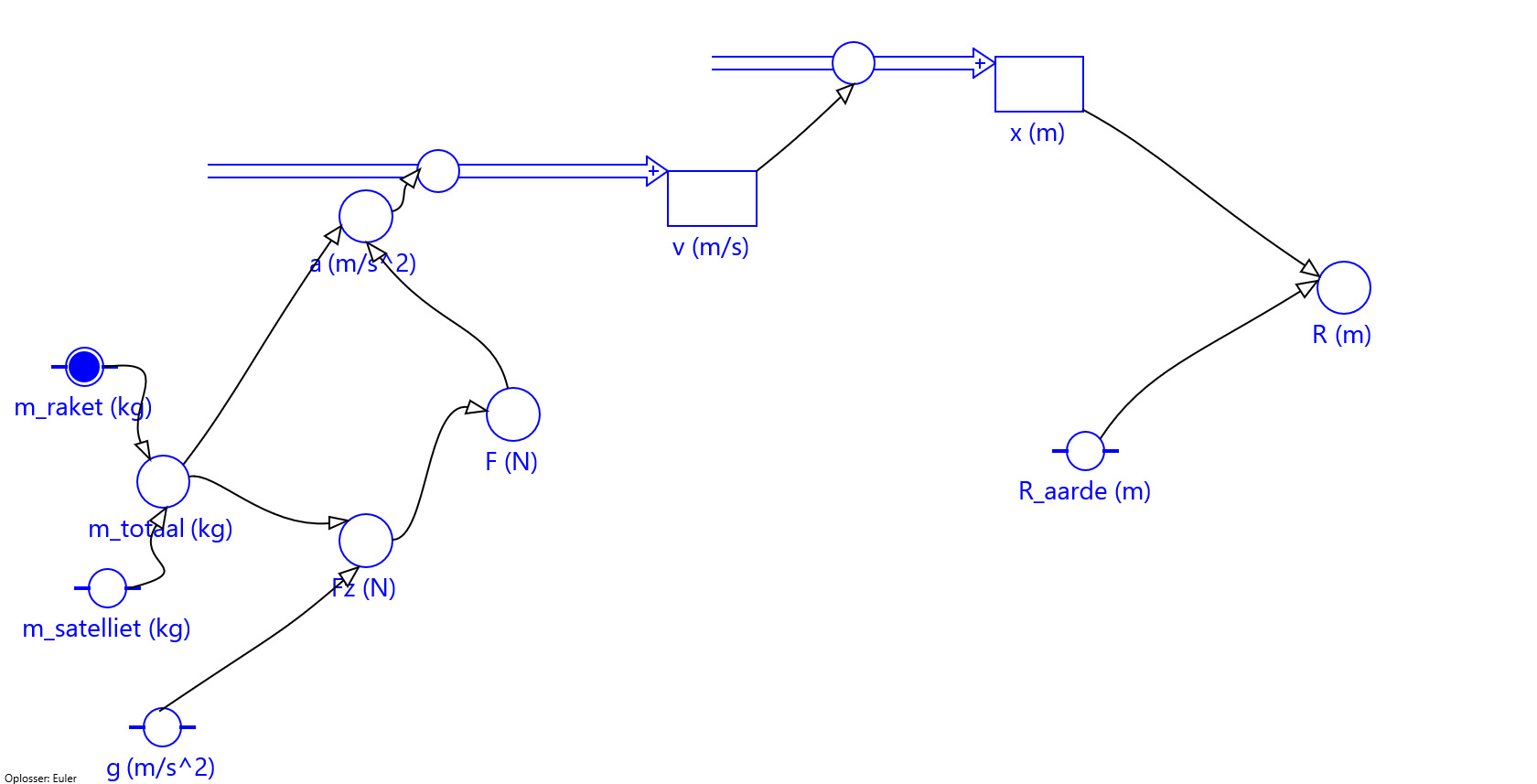

Haal het model raket01 op en bekijk het. Het is een model van een voorwerp dat met een beginsnelheid omhoog geschoten wordt, maar waarbij wel al rekening is gehouden met uitbreiding met andere krachten dan de zwaartekracht.
Bekijk het model, zorg dat je het begrijpt en speel er even mee.

Aanpassen met stuwkracht

Pas het model aan, zodat de raket stuwkracht krijgt en met een beginsnelheid van 0 m/s omhoog gaat.

Als het model een klein beetje de werkelijkheid moet nabootsen, moet je eerst goed over de situatie nadenken.

Het model verder invullen

Wat is een raket die de lucht ingaat, gezien vanuit een model?

Je hebt een satelliet met een omhulling voor het omhoog schieten.
Hij heeft brandstof nodig.
De brandstof zelf weegt ook.
Meer brandstof meenemen betekent grotere tanks en betekent meer massa voor de raket.
Er is een motor die een bepaalde stuwkracht levert.
Als de motor stuwkracht levert, wordt er brandstof verbruikt.
Als de brandstof op is, levert de motor geen stuwkracht meer.

raket, die een satelliet de lucht in moet schieten:

massa satelliet en omhulling en dergelijke = 635 kg
massa brandstof = 40000 kg
massa tank en motor = 0,2*brandstofmassa
Brandstofverbruik = 200 kg/s
geleverde kracht per verbruikte kg brandstof per seconde = 3000 m/s

Figuur 2: Gegevens van 'een' raket

Deze kenmerken van een raket betekenen dat het model flink aangepast moet worden. De raketeigenschappen moeten vertaald worden in regels voor het model. Verder moeten de startwaarden aangepast worden aan de nieuwe situatie.

Verander het model zodanig dat het rekening houdt met de raketeigenschappen.

Kom je er niet uit, vraag dan aan je docent om het model RAKET03.

Speel met het nieuwe model en kijk hoe het reageert op verandering van bijvoorbeeld de brandstofmassa.

Rekening houden met veranderende zwaartekracht

Hoe hangt de zwaartekracht af van de afstand tot de aarde? Bouw dit in je model in. Bereken de afstand boven de aarde voor een geostationaire baan.
Bepaal met het model hoeveel brandstof de raket nodig heeft om tot die hoogte te komen.

Wrijving van de atmosfeer

Zoek uit hoe de dichtheid van de lucht afhangt van de hoogte. Ga na hoe de wrijvingskracht van de lucht afhangt van de snelheid van de raket en bouw daarna de wrijving in in het model.
Onderzoek nu hoeveel brandstof extra nodig is om de satelliet in de geostationaire baan te brengen.

Ook de kosten in ogenschouw!

Raketmotoren zijn duur. Een kleinere motor gebruiken spaart wat brandstof doordat de motor lichter is en dat scheelt dubbel geld. Als we er vanuit gaan dat de prijs van een motor evenredig is met de stuwkracht, dan moet uit te vinden zijn welke motorvermogen het meest economisch ingezet kan worden voor de satelliet.

Neem aan dat de motor voor elke kg/s verbruikte brandstof € 1000,-- kost. De brandstof kost een € 4,-- per kg. Neem verder aan dat de massa van de motor zelf eveneens evenredig is met de stuwkracht en dat de nu gebruikte motor 2000 kg weegt.