Lichtabsorptie door een bos

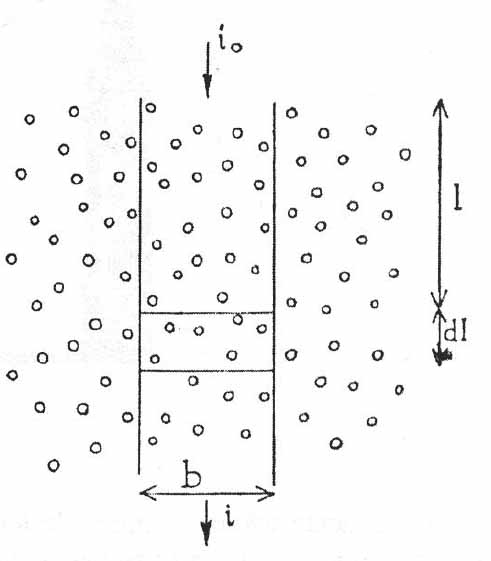
We gaan uit van een bos waarin de plaats van de bomen toevallig verdeeld is. Er komen in het bos \(N\) bomen per m² voor. Op ooghoogte is de diameter van de bomen \(D\).

Theorie

Kijk naar een bundel licht met breedte \(b\) die al over een lengte \(l\) door het bos is gegaan. Van de oorspronkelijke lichthoeveelheid \(i_{0}\) is nu nog maar \(i\) over.

Als de lichtstralen door eenzelfde dikte bos verder zouden gaan, zou dat deel bos eenzelfde percentage van dat licht weer weghalen. Deze manier van licht wegvangen door de bomen, waarbij een even dik stuk bos steeds een in verhouding even groot deel van het licht wegvangt, laat zich goed beschrijven met een exponentiele functie. Bij een donkere vloeistof werkt dat op soortgelijke manier, er komt minder licht door naarmate de laag vloeistof dikker is. Voor een bos levert dat op:

\(i=i_0 \cdot 10^{-0,43\cdot N \cdot D\cdot l}\)

Een dennenbos met een boom per m² en bomen met een diameter van 0,10 m, geeft dan bijvoorbeeld het volgende percentage nog doorgelaten licht:

De praktijk

Zo, nu wordt het eens tijd om aan de slag te gaan!

• Zoek met een groepje een stuk bos in een park. Het moet wel een stuk zijn dat aan één kant ophoudt.
• Bepaal in het door jouw groepje geselecteerd rechthoekig stuk park het aantal bomen per vierkante meter (\(=N\)) en meet de diameter (\(=D\)).
• Bepaal zo nauwkeurig mogelijk \(l\). (TIP: meet zo nauwkeurig mogelijk de lengte van één voetstap, tel het aantal voetstappen enz. enz.)
• Maak een schatting hoeveelste deel van buiten het bos je nog kunt zien.
• Bepaal de verhouding \(i/i_0\) met behulp van de gegeven formule. Een rekenmachine heb je nu echt wel nodig!
• Doe dit nog eens voor vier andere lengten, dus voor vier andere l's. Noteer alle gegevens in onderstaande tabel.
• Vergelijk de door jou geschatte en de berekende verhouding van het licht dat nog door het bos komt.