Wat is nu precies het verschil tussen massa en gewicht? Deze proef verheldert dat op basis van al bekende, eenvoudige ervaringen met een nieuwe interpretatie.
We zeggen vaak 'gewicht' als we 'massa' bedoelen. Natuurkundig gezien is 'gewicht' de kracht waarmee een voorwerp op zijn ondersteuning drukt, of daar aan trekt. Leerlingen onderscheiden massa en gewicht pas als ze daar een goede reden voor hebben. De ervaring van schommelen kan ze die reden geven.
De beschrijving van deze demo staat in het boek Showdefysica.
Als oriëntatie op de proef zijn de volgende discussievragen geschikt:
Merk op: alle vragen gaan over gewicht, maar de eerste drie gaan over hoeveel van iets er is (stof of materie), en de laatste drie gaan over wat je in sommige situaties voelt. Over het verschil tussen die twee gaat deze proef; het eerste noemen natuurkundigen massa, het tweede noemen ze gewicht.
Laat de leerlingen voorspellen:
Verder onderzoekDoor uitproberen kan onderzocht worden of er een relatie is tussen uitwijking, maximaal en minimaal gewicht (binnen de grenzen van veiligheid). Door extrapolatie of gedachtenexperiment kan nagegaan worden of er een situatie is waarin het gewicht nul zou worden.
Mocht het wat te bewerkelijk zijn om een schommel in de klas op te hangen of de proef in een speeltuin uit te voeren, maak dan met een gekantelde tafel of statieven een kleine schommel met een massa van bijvoorbeeld 200 g aan een veerunster of krachtsensor. Klem het statief dan wel goed vast op de tafel.
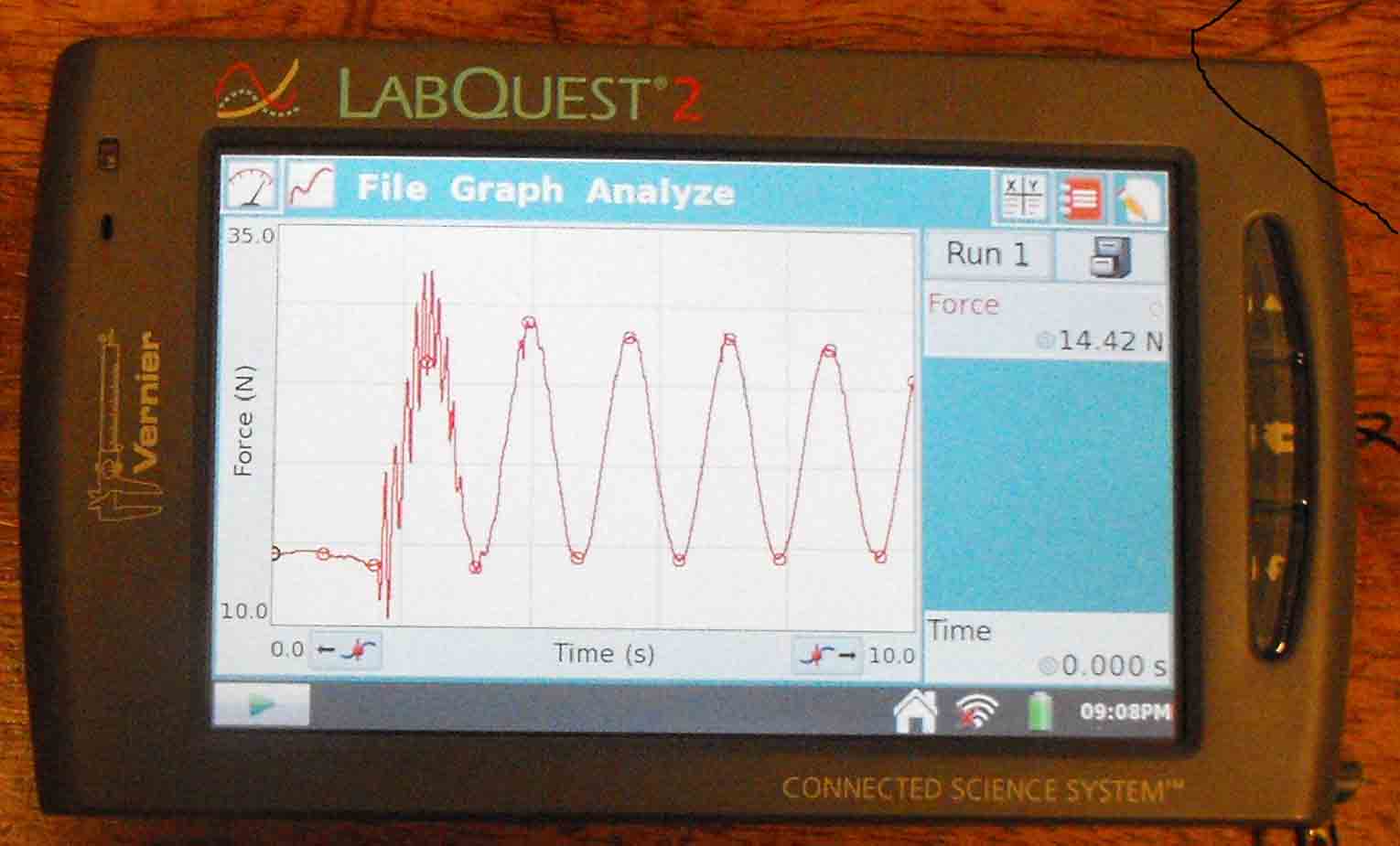Voor het gewicht en de massa van het blokje van 200 g geldt verder precies hetzelfde als voor het gewicht en de massa van een schommelaar. De metingen die in het boek beschreven worden, worden bij de mini-schommel aan het blokje gedaan: geef, na meting bij stilstand, de mini-schommel een behoorlijke beginuitwijking en laat hem los, registreer met het blote oog de maximale en minimale waarde, of meet met de krachtsensor hoe het gewicht varieert.
In het Angelsaksisch taalgebied wordt met 'weight' vaak bedoeld: de zwaartekracht. Wat wij 'gewicht' noemen wordt daar dan 'apparent weight' genoemd. Niet iedereen is het met die keuze eens (Warren, 1979). Ook in Nederland laait de discussie over 'gewicht' wel eens op. De betekenis van een woord is natuurlijk een arbitraire keuze, maar communiceren wordt wel wat lastig als we niet allemaal dezelfde keuze maken. De keuze die hier gemaakt is heeft als voordeel dat die overeenstemt met het begrip 'gewichtloos'; een astronaut in een rondcirkelende satelliet ondervindt wel de zwaartekracht maar oefent geen gewicht uit en is dus 'gewichtloos'. Net als iemand die een sprongetje maakt of valt.
De discussie kun je uitbreiden naar het begrip 'g-kracht', wat geen natuurkundig begrip is maar waar leerlingen in verband met kermistoestellen en attractieparken vaak wel van gehoord hebben. In lijn met deze proef zou ik de (dimensieloze) g-kracht definiëren als: gewicht gedeeld door zwaartekracht voor een willekeurige massa. In een eenparig bewegend stelsel is de g-kracht dus 1, en in vrije val 0. Als een systeem sneller valt dan vrije val wordt de g-kracht negatief. Maar in lijn met de Angelsaksische verwarring bestaat er ook alternatieve definities. Volgens Wikipedia is dan ook de bovenstaande definitie onjuist, en is de g-kracht gewoon de zwaartekracht (eenheid N). Weer anderen kiezen de g-kracht juist ten opzichte van rust: de g-kracht is dan 0 in een eenparig bewegend stelsel, en -1 in vrije val.
Ik wil u de prachtige constructie niet onthouden die door onze testers is uitgeprobeerd; zie de foto. Ook negatieve resultaten zijn immers waardevol, zowel in de wetenschap als het onderwijs. Zo vonden de testers dat de zaak gaat schuiven op deze parallellogram-schommel. Het ‘zitje’ blijft namelijk horizontaal, traagheid doet dan de rest. Ook werd gevonden dat de meeste elektronische meetinstrumenten te traag zijn voor metingen aan de schommel.
