Proef 4.2.3 Eenparig versneld lopen en diverse versnelde bewegingen

Proef 4.2.3a Eenparig versneld lopen

Benodigdheden:

• Een betegeld deel van een schoolplein of straat dat betegeld is met stoeptegels van 30cm x 30cm, een rij van tenminste 36 tegels (zie foto) (voor alternatief, indien geen betegeld stukje bij de school beschikbaar is: zie proef 4.2.1a)
• Stoepkrijt of bordkrijt
• Stopwatch (op mobiele telefoon)
• Een stuk touw van ca. 14 meter (niet al te dun, goed zichtbaar)

Voorbereiding:

Kies een lijn van 36 of meer stoeptegels en kies het startpunt s = 0 op de eerste voeg tussen 2 tegels. Teken daar een lijn en zet er START bij.

De baan bestaat uit 6 delen van toenemende grootte: zet bij de voeg na 1 tegel de letter A; zet bij de voeg 3 tegels verder een B; bij de voeg 5 tegels verder een C; D = 7 tegels verder; E = 9 tegels; F = 11 tegels.

Uitvoering 1: de beweging lopen

Instructie: Vraag een leerling bij de startlijn te gaan staan met de schoenpunt tegen de startlijn aan. Geef aan dat hij/zij na 1 s. met de schoenpunt bij voeg A moet zijn, na 2 s. bij B, na 3 s. bij C enz. tot punt F na 6 s. Geef aan dat jezelf de seconden van je stopwatch/telefoon hardop afleest.

Laat de leerling zo lopen en de beweging herhalen als die erg van het aangegeven schema tot t = 5 s afwijkt. Voeg F op tijd t = 6 s bereiken is lastig vanwege de hoge snelheid die daarvoor nodig is! Laat meerdere leerlingen deze beweging proberen te lopen.

Uitvoering 2: de snelheid tijdens de beweging

Analyseer de snelheid tijdens deze beweging met de leerlingen aan de hand van de volgende vragen:

1. Wat gebeurt er met je snelheid tijdens deze beweging?
2. Zit er een regelmaat in de toename van de snelheid? Welke?
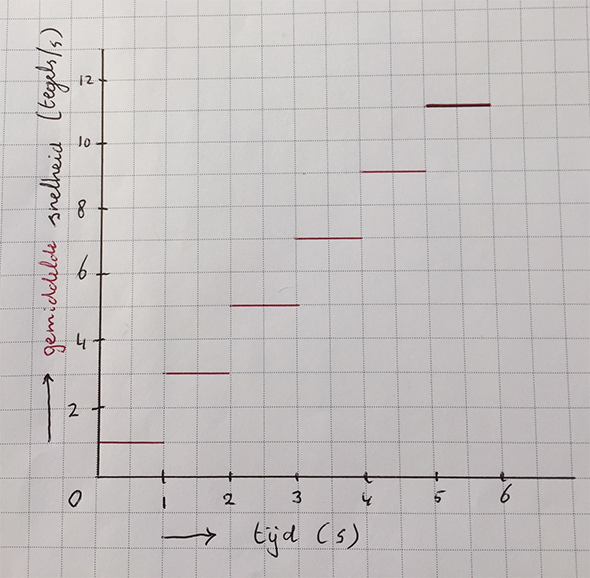
3. Laten we gaan kijken naar je gemiddelde snelheid in elke seconde: in de 1^e seconde? En in de 2^e? enz. [in de 1^e seconde: 1 tegel per seconde; in de 2^e seconde: 3 tegels per seconde; in de 3^e seconde: 5 tegels per seconde; ….. ]
4. Je kunt deze gemiddelde snelheden ook schrijven als:  in de 1^e s. (1 + 0x2) tegels/s; in de 2^e s. (1 + 1x2) tegels/s; in de 3^e s. (1 + 2x2) tegels/s enz. Dus elke seconde komen er 2  tegels/s bij.
5. Deze gemiddelde snelheden kunnen we in een v,t-diagram zetten. Zie foto links.

    

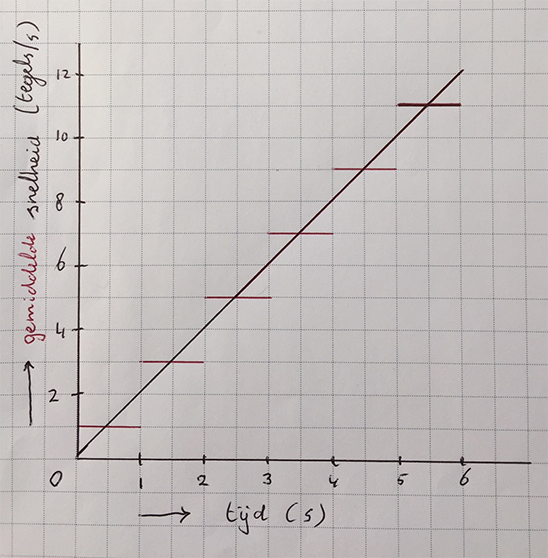
6. De snelheid zelf weten we alleen op t = 0: 0 m/s. We kunnen nu een rechte lijn tekenen door de middens van de lijntjes die de gemiddelde snelheden aangeven. Zie foto rechts. Met deze lijn kun je de snelheid op t = 1 s aflezen: 2 tegel/s. op t = 2 s is die snelheid toegenomen tot 4 m/s enz. Zo zie je ook dat de snelheid in elke seconde 2 tegels/s toeneemt.
7. Die toename van de snelheid noemen we de versnelling: de versnelling is hier dus een toename van 2 tegels/s per seconde. We moeten dus twee keer ‘per seconde’ zeggen. We noemen dat per seconde kwadraat: 2 tegels/s². Omgerekend naar meter krijgen we, omdat elke tegel 30 cm = 0,3 meter is: versnelling = 0,6 m/s²

Omdat de versnelling constant is, noemen we deze beweging eenparig versneld.

Uitvoering 3: Hoe neemt de afgelegde weg toe?

Deze uitvoering sluit aan bij paragraaf 2.5 van het boek.

Analyseer de verplaatsing (of afgelegde weg) tijdens deze beweging met de leerlingen aan de hand van de volgende vragen:

1. Waar zou het 7e punt G liggen? [op 13 tegels van F] En het 8^e punt H? [op 15 tegels van G] , …..
2. Welke regelmatigheid zit daarin? [de afgelegde weg neemt kwadratisch toe: s₁ = 1², s₂ = 2²,  s₃ = 3², enz.]
3. We kunnen nu een s,t diagram tekenen, met de s, de afgelegde weg.
   • Trek de s-as  en zet erbij: s in tegels. Geef de tegels 5, 10, 15 enz. aan en teken de punten A t/G in.
   • Trek de t-as en zet erbij t in s. Neem twee tegels voor 1 seconde. En geef de punten 1 tm 6 op de t-as aan.
   • Teken nu de punten in: punt A: s = 1 tegel op t = 1 s. Punt B: s = 4 tegels op t = 2 s enz.
4. Je ziet nu dat de s,t-grafiek een kromme is. Deze kromme heet in de wiskunde een parabool.

Proef 3M 2.3b Verschillende versnelde bewegingen

Laat de leerlingen enkele van de volgende situaties zien en vraag hen: is dit een versnelde beweging? Zo ja, kan het een eenparig versnelde beweging zijn? Waarom wel/niet?

1. Een karretje op de tafel wordt versneld door een zakkend gewicht aan een touw dat over een katrol is geslagen.
2. Een karretje rijdt vanuit stilstand een helling af.
3. Een speelgoedautootje met een inwendige veer wordt een stukje achteruit gereden (de veer wordt gespannen) en dan losgelaten. Het autootje versnelt en vertraagt vervolgens.
4. Een Chinees hoedje van papier wordt op een hoogte losgelaten en valt na enige tijd met een constante snelheid. Zie ook proef 2M 1.6b voorhet maken van een hoedje
5. Een steentje of knikker wordt op een hoogte losgelaten en valt steeds sneller.