Doel van de proef: de leerlingen weten dat op een voorwerp op een helling een normaalkracht werkt die loodrecht staat op het hellingsvlak en die kleiner is dan de zwaartekracht op het voorwerp. Ze kunnen de zwaartekrachtsvector ontbinden in twee componenten, een langs en de andere loodrecht op de helling.
Zie de foto’s hieronder voor een mogelijke uitvoering van de proef.
Foto 1: De wagen (massa 50 gram) staat op een helling en wordt tegengehouden door een veerunster die vastzit aan een spijker.
Foto 2: De wagen is verzwaard met twee massastukken: een van 100 gram en een van 50 gram.
Foto 3: De massa van het geheel is dus 200 gram = 0,20 kg. De zwaartekracht op de wagen is dus Fz = 0,20 * 10 = 2,0 N. Hij is naar beneden gericht en grijpt aan op het zwaartepunt van de wagen. We geven die weer met een vectorpijl van 2 dm. Om praktische redenen is deze pijl op de foto in de zijkant van de helling geprikt.
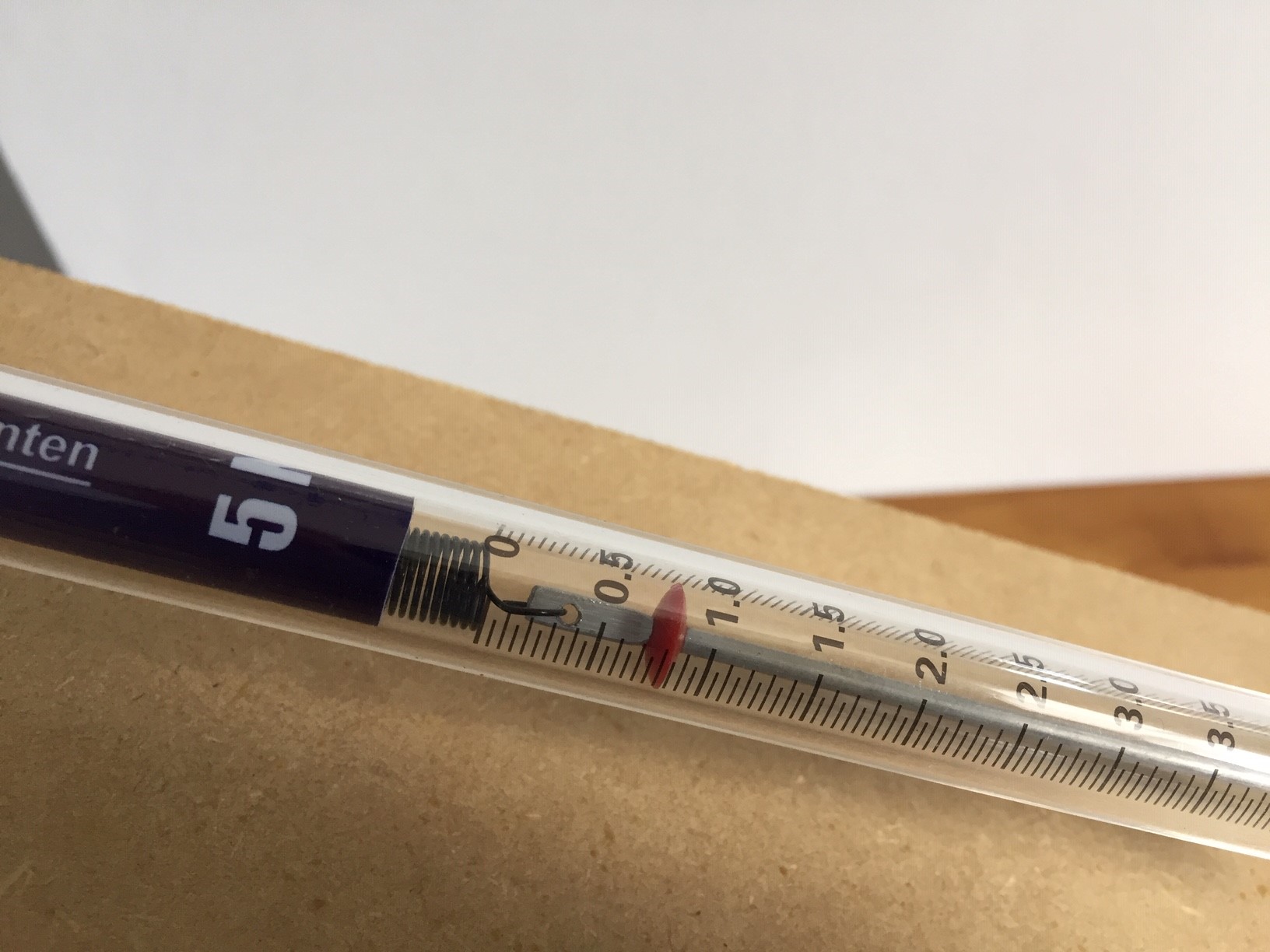Foto 4: De veerunster geeft 0,8 N aan. We nemen aan dat er geen wrijvingskracht op de wagen werkt.
Foto 5: De wagen ondervindt dus een kracht van 0,8 N langs de helling omhoog, die we met een vectorpijl van 0,8 dm weergegeven en die we ook in het zwaartepunt laten aangrijpen.
Foto 6: Omdat de wagen stil staat, moet de kracht door de veerunster volgens de wetten van Newton opgeheven worden door een even grote kracht langs de helling omlaag. Deze kracht is een component van de zwaartekracht. Daarom is de vectorpijl gestippeld en in het rood aangegeven.
Foto 7: Om de andere component van de zwaartekracht te vinden, moeten we de component langs de helling naar beneden vectorieel aftrekken van de zwaartekracht. Dat kan door de pijlpunten van de twee vectoren met elkaar te verbinden. Zoal op de foto te zien is, staat die tweede component van de zwaartekracht loodrecht op de helling. Opmeting geeft een lengte van 18 cm = 1,8 dm. Deze component is dus 1,8 N.
Foto 8: De tweede component van de zwaartekracht grijpt op hetzelfde punt aan als de zwaartekracht.
Foto 9: Omdat de wagen stil staat, moet die component loodrecht op de helling opgeheven worden door een kracht. Die kracht staat loodrecht op de helling omhoog. Hij heet de normaalkracht. Op de foto zie je dat de normaalkracht en de kracht door de unster opgeheven worden door de componenten van de zwaartekracht.
Foto 10: Op de foto zijn de componenten niet weergegeven, maar de zwaartekracht zelf wel.
Conclusie
Op een stilstaand voorwerp op een helling werken dus ten minste drie krachten: een langs de helling omhoog, een loodrecht op de helling naar boven (de normaalkracht) en de zwaartekracht natuurlijk. Er kunnen nog meer krachten werken, een wrijvingskracht bijvoorbeeld.
